Unidad 1 Examen Introduccion al Algebra Lineal *
Revisión del intento 2
| JESUS OYENTE MATA CASTRO | |
| Intentos | 1, 2 |
| Comenzado el | miércoles, 16 de mayo de 2012, 10:06 |
| Completado el | miércoles, 16 de mayo de 2012, 11:02 |
| Tiempo empleado | 55 minutos 10 segundos |
| Calificación | 10.667 de un máximo de 10 (107%) |

| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | 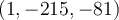 | 10:12:40 on 16/05/12 | 1 | 0 |
| 2 | Cerrar | 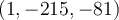 | 11:02:00 on 16/05/12 | 1 | 1 |
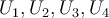 en el ORDEN INDICADO.
en el ORDEN INDICADO.Si decide que el conjunto
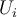 SI es subespacio de
SI es subespacio de 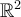 debera indicarlo con: 1
debera indicarlo con: 1Si decide que el conjunto
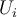 NO es subespacio de
NO es subespacio de 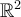 debera indicarlo con: 0
debera indicarlo con: 0Decida si cada uno de los conjunto es o no un subespacio de
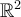
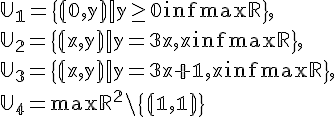
Su respuesta debera indicarla en la siguiente forma: 1101

| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | 0100 | 10:12:40 on 16/05/12 | 1 | 0 |
| 2 | Cerrar | 0100 | 11:02:00 on 16/05/12 | 1 | 1 |
Decida si cada una de las proposiciones es falsa o verdadera, o bien ninguna de estas opciones.
Considere la ecuacion matricial 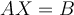 y sea
y sea ![[A|B] [A|B]](http://galois.azc.uam.mx/filter/tex/pix.php/d120aea4fc70498ed6454d3444a254c0.png) la matriz aumentada del sistema de m ecuaciones con n variables.
la matriz aumentada del sistema de m ecuaciones con n variables.
| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | 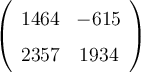 , , | 10:15:32 on 16/05/12 | 1 | 0 |
| 2 | Cerrar | 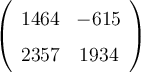 , , | 11:02:00 on 16/05/12 | 1 | 1 |
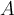

Un conjunto de generadores del Espacio Fila de
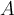
Un conjunto de generadores del Espacio Columna de
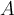
Un conjunto de generadores del Espacio Nulo de
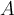
Un conjunto de generadores del Espacio Nulo Izquierdo de
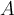 son RESPECTIVAMENTE:
son RESPECTIVAMENTE: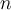 adecuado, diga si
adecuado, diga si  es un subespacio de
es un subespacio de  .
.Si su respuesta es afirmativa, debera poner en el cajon de respuestas, sin usar comas, ni puntos, ni espacios, y en mayusculas la palabra:
SI
Importante, el robot busca precisamente estos caracteres, si usted pone por ejemplo "Si", "SI." ,
""Si es espacio vectorial", "SI " (note aqui hay un espacio), en todos estos casos, el robot considerara que
su respuesta es incorrecta.
Si su respuesta es negativa, debera poner en el cajon de respuestas, sin usar comas, ni puntos, ni espacios, y en mayusculas la cadena de caracteres:
NO
Importante, el robot busca precisamente estos caracteres, si usted pone por ejemplo "No", "NO." ,
""No es espacio vectorial", "NO " (note aqui hay un espacio), en todos estos casos, el robot considerara que
su respuesta es incorrecta.

| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | NO | 10:25:03 on 16/05/12 | 1 | 0 |
| 2 | Cerrar | NO | 11:02:00 on 16/05/12 | 1 | 1 |
Considere el espacio vectorial de matrices  con las operaciones usuales. Tenemos la siguiente combinacion lineal de vectores:
con las operaciones usuales. Tenemos la siguiente combinacion lineal de vectores:
Encuentre los escalares 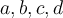 que hacen posible la combinacion lineal anterior.
que hacen posible la combinacion lineal anterior.
Instrucciones para este ejercicio.
Sus respuestas deberan ser escritas en las cajas correspondientes sin poner espacios, sin el simbolo "=", sin comas, sin puntos. En caso de numero negativo, debera poner el signo "menos" dentro de la caja. Si su resultado es una fraccion, debera reducirla y ponerla en la forma m/n dentro de la caja correspondiente. Ejemplo -4/8 debe escribir: -1/2
| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | -4/3, -22/3, -5/3, 6 | 10:25:03 on 16/05/12 | 4 | 0 |
| 2 | Cerrar | -4/3, -22/3, -5/3, 6 | 11:02:00 on 16/05/12 | 4 | 4 |
| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | $$A$$ es linealmente dependiente si y solo si existe $$v \in A$$ que es ... | 10:27:07 on 16/05/12 | 1 | 0 |
| 2 | Guardar | $$A$$ es linealmente dependiente si y solo si existe $$v \in A$$ que es ... | 10:33:01 on 16/05/12 | 1 | 0 |
| 3 | Cerrar | $$A$$ es linealmente dependiente si y solo si existe $$v \in A$$ que es ... | 11:02:00 on 16/05/12 | 1 | 1 |
 ,
, ,
, ,
,Cual de las siguientes matrices SI se encuentra en el espacio generado por los vectores
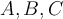 ?
?| # | Acción | Respuesta | Fecha | Puntuación bruta | Calificación |
|---|---|---|---|---|---|
| 1 | Guardar | 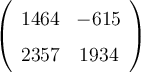 , , | 10:33:01 on 16/05/12 | 1 | 0 |
| 2 | Cerrar | 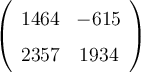 , , | 11:02:00 on 16/05/12 | 1 | 1 |
Denotemos por 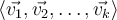 el espacio generado por los vectores
el espacio generado por los vectores 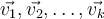 .
.
Encuentre las componentes 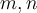 del vector indicado a continuación, de tal forma que se tenga la igualdad de espacios vectoriales:
del vector indicado a continuación, de tal forma que se tenga la igualdad de espacios vectoriales:
Instrucciones para este ejercicio.
Sus respuestas deberan ser escritas en las cajas correspondientes sin poner espacios, sin el simbolo "=", sin comas, sin puntos. En caso de numero negativo, debera poner el signo "menos" dentro de la caja. Si su resultado es una fraccion, debera reducirla y ponerla en la forma m/n dentro de la caja correspondiente. Ejemplo -4/8 debe escribir: -1/2

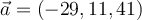
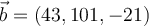
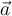
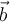
![Rango[A|B]=Rango[A] Rango[A|B]=Rango[A]](http://galois.azc.uam.mx/filter/tex/pix.php/9605c927adcac96a4a3f3c8ccf2f7de3.png)
![Rango[A|B]=Rango[A|B] Rango[A|B]=Rango[A|B]](http://galois.azc.uam.mx/filter/tex/pix.php/96eb2ca5d0dedadbfc387096c9e561ca.png)
![Rango[A|B]+1=Rango[A]+1 Rango[A|B]+1=Rango[A]+1](http://galois.azc.uam.mx/filter/tex/pix.php/4a51ecb440ece7b4ecdee929b2d6d6e0.png)

![L[A,B,C] L[A,B,C]](http://galois.azc.uam.mx/filter/tex/pix.php/f48c9ff915ad4341fb269488f8009cec.png)


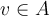
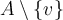
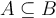
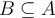
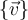
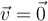
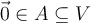
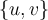
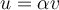

 Moodle Docs para esta página
Moodle Docs para esta página